Dokaz formule za \(\dfrac{\pi}{2\sqrt{3}}\)

 Pozdrav svima . Danas ćemo dokazati formulu za   \(\dfrac{\pi}{2\sqrt{3}}\). Kao dokazni metod koristićemo metod direktnog dokaza. Teorema 1:  \[\frac{\pi}{2\sqrt{3}}=\displaystyle\sum_{n=1}^{\infty}\frac{\chi(n)}{n}\]\[\text{gde je} \quad \chi(n)=\begin{cases} 1, & \text{if } n \equiv 1 \pmod{6}\\-1, & \text{if } n \equiv -1 \pmod{6}\\0, & \text{inače}\end{cases}\] Teorema 2: Imamo \[\frac{\pi}{2\sqrt{3}}=\frac{5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot 29 \cdots}{6 \cdot 6 \cdot 12 \cdot 12 \cdot 18 \cdot 18 \cdot 24 \cdot 30 \cdots}\]izraz čiji su brojioci sekvenca neparnih prostih brojeva većih od \(3\) i čiji su imenioci parni brojevi koji su za jedan veći ili manji od odgovarajućih brojilaca. Dokaz: Na osnovu Teoreme 1 znamo da je \[\frac{\pi}{2\sqrt{3}}=1-\frac{1}{5}+\frac{1}{7}-\frac{1}{11}+\frac{1}{13}-\frac{1}{17}+\frac{1}{19}-\cdots\] takođe imamo \[\frac{1}{5} \cdot \frac{\pi}{2\sqrt{3}}=\frac{1}{5}-\frac{1}{25}+\frac{1}{35}-\frac{1}{55}+\cdot
Постави коментар

Dokaz kosinusne teoreme

 Pozdrav svima. Danas ćemo dokazati kosinusnu teoremu. Kao dokazni metod koristićemo metod direktnog dokaza. Ovu teoremu je prvi formulisao persijski matematičar Kašani.

Teorema: Neka su \(a,b,c\) stranice bilo kog trougla i neka su uglovi \(\alpha,\beta,\gamma\) uglovi naspram stranica \(a,b,c\) , redom. Tada važe sledeće jednakosti:\[c^2=a^2+b^2-2ab\cos \gamma\]\[b^2=a^2+c^2-2ac\cos \beta\]\[a^2=b^2+c^2-2bc\cos \alpha\]

Dokaz:

Sada ćemo izvesti dokaz da važi jednakost:\[c^2=a^2+b^2-2ab\cos \gamma\]Ostale dve jednakosti se dokazuju na analogan način.

Postoje tri moguća slučaja, a to su: \( \gamma\) je prav ugao, \( \gamma\) je oštar ugao i \( \gamma\) je tup ugao.

Prvi slučaj: \( \gamma=90^{\circ}\)

Na osnovu Pitagorine teoreme znamo da za pravougli trougao sa hipotenuzom \( c\) važi jednakost: \[c^2=a^2+b^2\] Sa druge strane kako je \( \cos\gamma=\cos 90^{\circ}=0\) važi da je:\[c^2=a^2+b^2-0\]\[c^2=a^2+b^2-2ab\cos 90^{\circ}\]\[c^2=a^2+b^2-2ab\cos \gamma\]

Drugi slučaj: \( \gamma<90^{\circ}\)

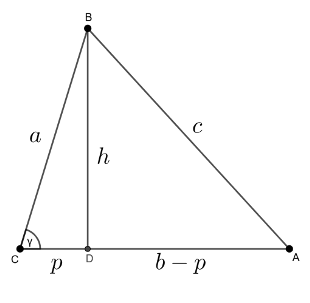
Posmatrajmo sledeći dijagram na kom se nalazi oštrougli trougao \(\triangle ABC\) sa visinom \(h\).

Na osnovu Pitagorine teoreme možemo zapisati sledeće dve jednakosti:

\[a^2=h^2+p^2\]\[c^2=h^2+(b-p)^2\]

Kombinujući ove dve jednakosti dobijamo:\[c^2=a^2-p^2+(b-p)^2\]\[c^2=a^2-p^2+b^2-2bp+p^2\]\[c^2=a^2+b^2-2bp\]Kako je \( p=a\cos\gamma\) imamo: \[c^2=a^2+b^2-2ab\cos \gamma\]

Treći slučaj: \( \gamma>90^{\circ}\)

Posmatrajmo sledeći dijagram na kom se nalazi tupougli trougao \(\triangle ABC\) sa visinom \(h\).

Na osnovu Pitagorine teoreme možemo zapisati sledeće dve jednakosti:\[a^2=h^2+p^2\]\[c^2=h^2+(b+p)^2\]Kombinujući ove dve jednakosti dobijamo:\[c^2=a^2-p^2+(b+p)^2\]\[c^2=a^2-p^2+b^2+2bp+p^2\]\[c^2=a^2+b^2+2bp\]Kako je \(p=a \cos \left(180^{\circ}-\gamma\right)\) imamo:\[c^2=a^2+b^2+2ab \cos\left(180^{\circ}-\gamma\right)\]Primenjujući identitet \(\cos\left(180^{\circ}-\gamma\right)=-\cos \gamma\) dobijamo: \[c^2=a^2+b^2-2ab\cos \gamma\]

\(\blacksquare\)

Коментари

Постави коментар

Популарни постови са овог блога

Dokaz da je koren iz prostog broja iracionalan broj

Pozdrav svima. Danas ćemo dokazati da je kvadratni koren iz prostog broja iracionalan broj. Kao dokazni metod koristićemo metod kontradikcije. Teorema: Ako je \(p\) prost broj, tada je \(\sqrt{p}\) iracionalan broj. Dokaz:  Pretpostavimo suprotno, tj. da je \(\sqrt{p}\) racionalan broj. Tada \(\sqrt{p}\) možemo zapisati u obliku razlomka \(\frac{a}{b}\), gde su \(a\) i \(b\) dva uzajamno prosta cela broja i \(b \neq 0\). Kvadriranjem jednakosti \(\sqrt{p}=\frac{a}{b}\) dobijamo jednakost \(p=\frac{a^2}{b^2}\), odnosno \(a^2=pb^2\). Zapišimo sad brojeve \(a\) i \(b\) u obliku proizvoda stepenova njihovih prostih faktora.\[a=p_1^{n_1}\cdot p_2^{n_2} \cdot p_3^{n_3} \cdot \ldots \cdot p_j^{n_j}\]\[b=q_1^{m_1}\cdot q_2^{m_2} \cdot q_3^{m_3} \cdot \ldots \cdot q_k^{m_k}\]Kvadriranjem ove dve jednakosti dobijamo:\[a^2=p_1^{2n_1}\cdot p_2^{2n_2} \cdot p_3^{2n_3} \cdot \ldots \cdot p_j^{2n_j}\]\[b^2=q_1^{2m_1}\cdot q_2^{2m_2} \cdot q_3^{2m_3} \cdot \ldots \cdot q_k^{2m_k}\]Kako je \(a^2=pb^
Прикажи све

Dokaz da je koren iz 2 iracionalan broj

Pozdrav svima. Danas ćemo dokazati da je \(\sqrt{2}\) iracionalan broj. Kao dokazni metod koristićemo metod kontradikcije. Ovaj dokaz je prvi izveo grčki filozof Aristotel. Teorema:  \(\sqrt{2}\)  je iracionalan broj. Dokaz: Pretpostavimo da je \(\sqrt{2}\) racionalan broj. Tada \(\sqrt{2}\) možemo zapisati u obliku \( \frac{p}{q} \) gde su \( p \)  i \( q\) uzajamno prosti  celi brojevi takvi da \(q \neq 0\). Primetimo da kako je \( \frac{p}{q} \) nesvodljiv razlomak \( p \) i \( q \) ne mogu istovremeno biti parni inače razlomak ne bi bio nesvodljiv. Iz jednakosti \(\sqrt{2}=\frac{p}{q}\) sledi da je \(2=\frac{p^2}{q^2}\) odnosno \( p^2=2q^2\) . Dakle \(p^2\) je paran broj odakle sledi da je \(p\) takođe paran broj pa možemo broj \(p\) zapisati u obliku \(p=2k\) gde je \(k\) celi broj.  Dakle, imamo da je \( (2k)^2=2q^2\) tj. \( 4k^2=2q^2\), odnosno \( q^2=2k^2\). Iz poslednje jednakosti zaključujemo da je \(q^2\) paran broj, pa je samim tim i \( q\) paran broj. Pokazali smo da su \(
Прикажи све

Dokaz da je skup prostih brojeva beskonačan

 Pozdrav svima. Danas ćemo dokazati da je skup prostih brojeva beskonačan. Kao dokazni metod koristićemo metod kontradikcije. Takođe ćemo upotrebiti teoremu francuskog matematičara Eduarda Lukasa. Teorema (Lukas): Svaki prost faktor Fermaovog broja \(F_n=2^{2^n}+1\) ; (\(n>1\)) je oblika \(k2^{n+2}+1\) . Teorema: Skup prostih brojeva je beskonačan. Dokaz: Pretpostavimo suprotno, da postoji samo konačno mnogo prostih brojeva i označimo najveći prosti broj sa \(p\) . Tada je \(F_p\) sigurno složen broj jer je \(F_p > p\) . Na osnovu Lukasove teoreme znamo da postoji prost broj \(q\) koji je oblika   \(k2^{p+2}+1\)  i koji deli broj \(F_p\). Ali \(q > p\) što je u kontradikciji sa polaznom pretpostavkom. Dakle, skup prostih brojeva je beskonačan . \(\blacksquare\)
Прикажи све